Instead of using five rules to determine the regularity of a polyhedron, is repetition within a polyhedron of essential importance for the regularity index. Something is more or less regular if it shows more or less repetitions. Within a polyhedron you can find repetitions. For instance a cube: this polyhedron can have 24 different positions, while it does look completely the same cube. This is illustrated in the figure below. A cube has therefore 24 'positions of equality'.

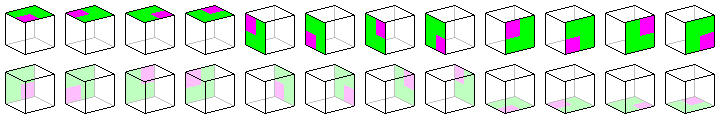
Since the dual of a cube is an octahedron, can you expect that an octahedron has also 24 positions of equality. You can see that this is true in the graph below. 

The tetrahedron, the smallest possible polyhedron has just twelve positions of equality. That this number is less than in a cube or octahedron is quite logical, since a tetrahedron has less faces, vertexes and edges. 

What do these 'positions of equality' have to do with the regularity index? The answer on this question is: everything. As shown above is the number of positions of equality not the same in every polyhedron, it also depends on the number of faces/edges/vertexes of a polyhedron. The higher the number of faces/edges/vertexes, the more positions of equality are theoretically possible. 

The regularity index in the relation between the number of positions of equality (nP) and the number of edges (nR). So in a formula:

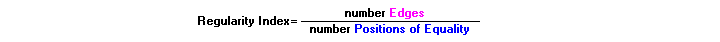
The number of edges has been chosen because this number reflects the complexity of a polyhedron better than the number of faces or vertexes. Beside this is the number of edges related to the number of the other two, since the number of edges is formed by the sum of the number of faces and vertexes minus two. 

The formula for the regularity index could be simplified written by:

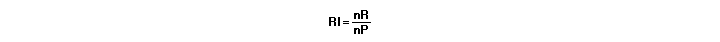
If you now face the cube, than he number of positions of equality is 24, then number of edges is 12, so the regularity index (RI) is 0.5. Both the tetrahedron and octahedron do also have a RI of 0.5. 

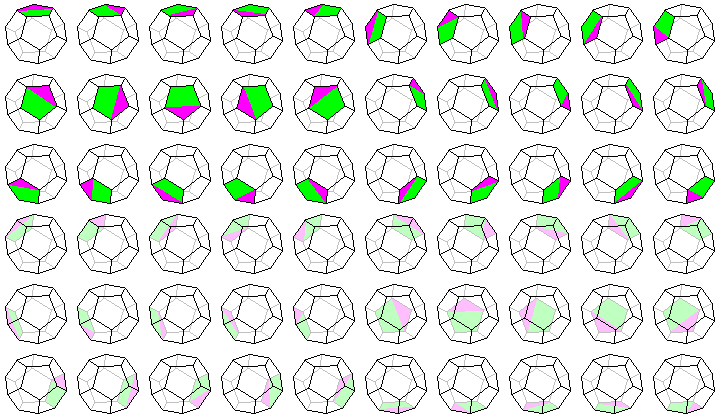
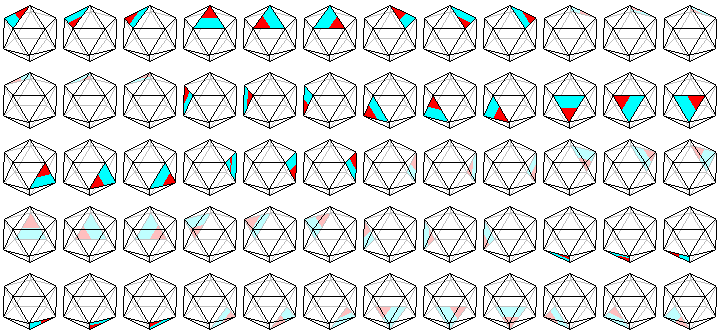
The number of positions of equality of a dodecahedron and icosahedron is 60 in both polyhedra (see illustrations below). Both polyhedra do have 30 edges, so both polyhedra do have a regularity index of 0.5. Apparently is the regularity index in all Platonic polyhedra 0.5. A lower regularity index is not possible, so a regularity index of 0.5 is correspond to complete regular polyhedra. 

The higher the regularity index, the more irregular the polyhedron is. The maximum of the regularity index is bounded to the number of edges of a polyhedron. The regularity index cannot be higher than the number of edges. Under the tab 'examples' you can find some examples on regularity index. It will be made clear that the regularity index says more about how regular a polyhedron is than the five rules described before.